求二叉搜索树的第 K 小的值

题目

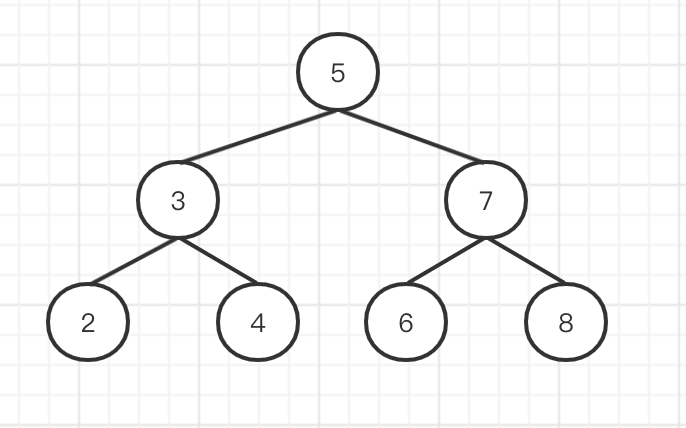
一个二叉搜索树，求其中的第 K 小的节点的值。 如下图，第 3 小的节点是 4

二叉树

树，大家应该都知道，如前端常见的 DOM 树、vdom 结构。

二叉树，顾名思义，就是每个节点最多能有两个子节点。

interface ITreeNode {
    value: number // 或其他类型
    left?: ITreeNode
    right?: ITreeNode
}

二叉树的遍历

• 前序遍历：root -> left -> right
• 中序遍历：left -> root -> right
• 后序遍历：left -> right -> root

二叉搜索树 BST

• 左节点（包括其后代） <= 根节点
• 右节点（包括其后代） >= 根节点

思考：BST 存在的意义是什么？—— 后面解释

分析题目

根据 BST 的特点，中序遍历的结果，正好是按照从小到大排序的结果。
所以，中序遍历，求数组的 arr[k] 即可。

答案

代码 binary-search-tree-k-value.ts

export interface ITreeNode {
    value: number
    left: ITreeNode | null
    right: ITreeNode | null
}

const arr: number[] = []

/**
 * 二叉树前序遍历
 * @param node tree node
 */
function preOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    // console.log(node.value)
    arr.push(node.value)
    preOrderTraverse(node.left)
    preOrderTraverse(node.right)
}

/**
 * 二叉树中序遍历
 * @param node tree node
 */
function inOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    inOrderTraverse(node.left)
    // console.log(node.value)
    arr.push(node.value)
    inOrderTraverse(node.right)
}

/**
 * 二叉树后序遍历
 * @param node tree node
 */
function postOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    postOrderTraverse(node.left)
    postOrderTraverse(node.right)
    // console.log(node.value)
    arr.push(node.value)
}

/**
 * 寻找 BST 里的第 K 小值
 * @param node tree node
 * @param k 第几个值
 */
export function getKthValue(node: ITreeNode, k: number): number | null {
    inOrderTraverse(node)
    return arr[k - 1] || null
}

const bst: ITreeNode = {
    value: 5,
    left: {
        value: 3,
        left: {
            value: 2,
            left: null,
            right: null
        },
        right: {
            value: 4,
            left: null,
            right: null,
        }
    },
    right: {
        value: 7,
        left: {
            value: 6,
            left: null,
            right: null
        },
        right: {
            value: 8,
            left: null,
            right: null
        }
    }
}

// preOrderTraverse(bst)
// inOrderTraverse(bst)
// postOrderTraverse(bst)

console.log(getKthValue(bst, 3))

#

import { ITreeNode, getKthValue } from './binary-search-tree'

describe('二叉搜索树', () => {
    const bst: ITreeNode = {
        value: 5,
        left: {
            value: 3,
            left: {
                value: 2,
                left: null,
                right: null
            },
            right: {
                value: 4,
                left: null,
                right: null,
            }
        },
        right: {
            value: 7,
            left: {
                value: 6,
                left: null,
                right: null
            },
            right: {
                value: 8,
                left: null,
                right: null
            }
        }
    }

    it('正常情况', () => {
        const res = getKthValue(bst, 3)
        expect(res).toBe(4)
    })

    it('k 不再正常范围之内', () => {
        const res1 = getKthValue(bst, 0)
        expect(res1).toBeNull()

        const res2 = getKthValue(bst, 1000)
        expect(res2).toBeNull()
    })
})

划重点

• 二叉搜索树的特点
• 前序、中序、后序遍历